LIGHT

REFLECTION OF LIGHT

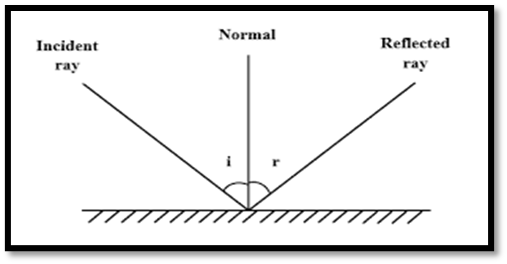
Reflection is the bouncing back of light rays in the same medium after hitting a smooth surface.

LAWS OF REFLECTION:

• The angle of incidence is equal to the angle of reflection

(∠𝑖=∠𝑟).

• The incident ray, the reflected ray, and the normal at the point of incidence all lie in the same plane.

IMAGE FORMATION:

If light rays meet or appear to meet at a point after reflection, the image is formed at that point.

TYPES OF IMAGES:

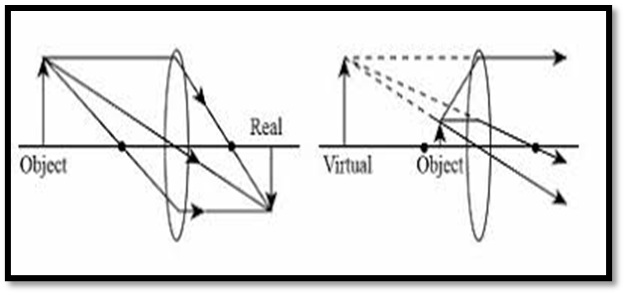
• Real Image: Light rays actually meet; can be displayed on a screen.
• Virtual Image: Light rays appear to meet; cannot be displayed on a screen.

Mirror

A mirror is a polished surface that reflects almost all incident light.

TYPES OF MIRRORS:

Plane Mirror: Has a flat reflecting surface, leads to the formation of virtual images.

• PLANE MIRRORS:

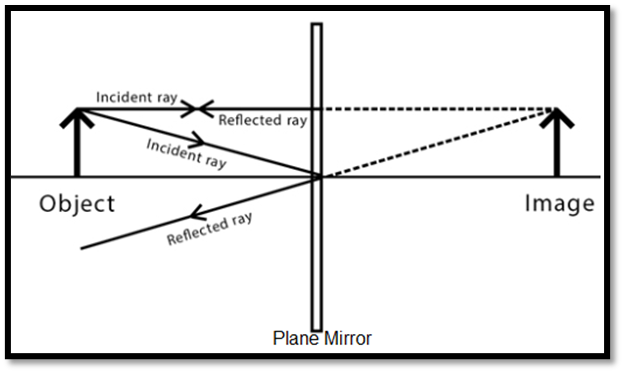
Properties:

• The image is virtual, erect, and formed behind the mirror.
• The size of the image equals the size of the object.
• The distance between the image and the mirror equals the distance between the object and the mirror.
• The image is laterally inverted.
• The focal length is infinite.

Uses:

Commonly used as looking glasses, in periscopes, and kaleidoscopes.

SPHERICAL MIRRORS:

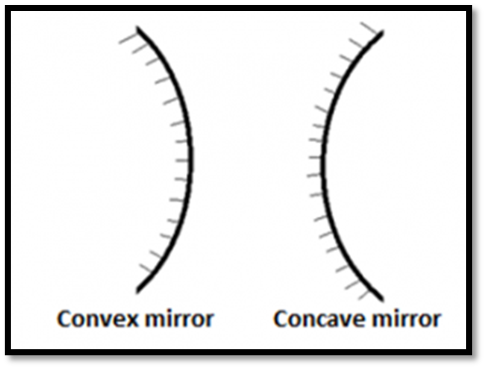
Types:

Concave Mirror:

• Reflecting surface is curved inwards.
• Converges light rays to a point.
• Examples include the inner surface of a spoon.

Convex Mirror:

• Reflecting surface is curved outwards.
• Diverges light rays.
• Examples include the outer surface of a spoon

DEFINITIONS:

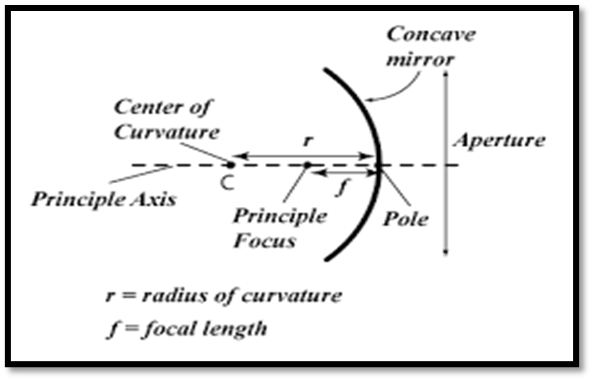
Centre of Curvature: Centre of the imaginary sphere; denoted by C.

Radius of Curvature: Radius of the imaginary sphere; denoted by R.

Pole: Mid-point of the reflecting surface; denoted by P.

Principal Axis: Line joining the pole and the centre of curvature.

Aperture: Diameter of the reflecting surface.

Principal Focus of a Spherical Mirror

• Concave Mirror: The principal focus is where parallel rays converge after reflection.
• Convex Mirror: The principal focus is where parallel rays appear to diverge after reflection.

Focal Length

• The distance between the pole and the principal focus.
• Denoted by 𝑓.
• For small apertures, 𝑓=𝑅/2where R is the radius of curvature.
• The focus of a concave mirror is real, while for a convex mirror, it is virtual.

• RAY DIAGRAMS FOR IMAGE FORMATION

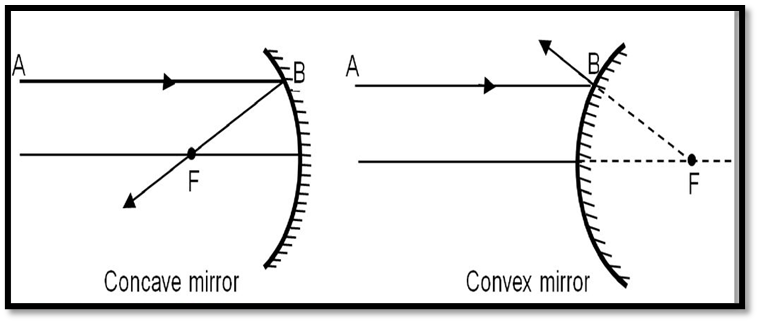
1. Parallel Rays: Rays parallel to the principal axis pass through the focus for a concave mirror or appear to diverge for a convex mirror.
2. Focus Rays: Rays through the focus of a concave mirror or directed towards the focus of a convex mirror become parallel after reflection.
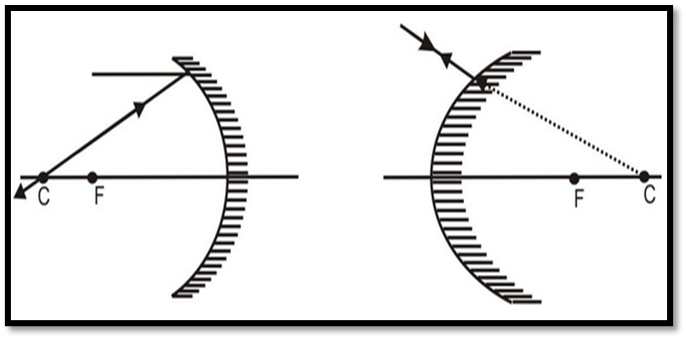
3. Centre of Curvature Rays: Rays passing through the centre of curvature reflect back along the same path.

1. Oblique Rays: Rays incident obliquely follow the laws of reflection.

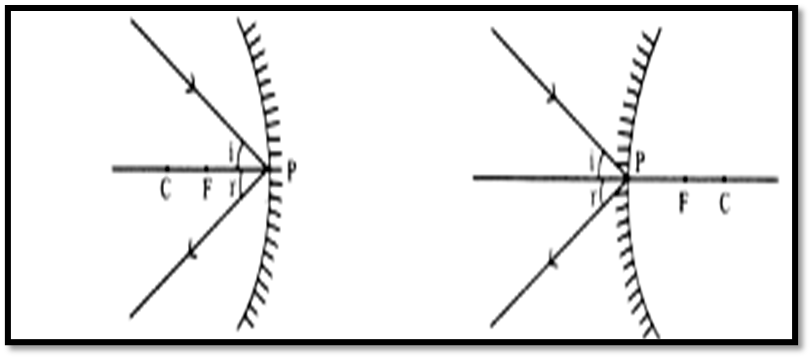
IMAGE FORMATION BY A CONCAVE MIRROR

• Position of Object: At Infinity.
• Position of Image: At focus or in the focal plane.
• Nature and Size: Real, inverted, and extremely diminished.

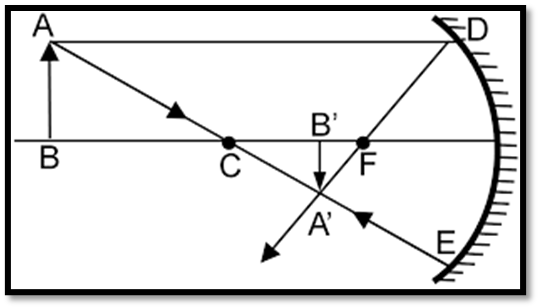
• Position of Object: Beyond the Centre of Curvature
• Position of Image: Between focus and centre of Curvature.
• Nature and Size: Real, inverted, and diminished.

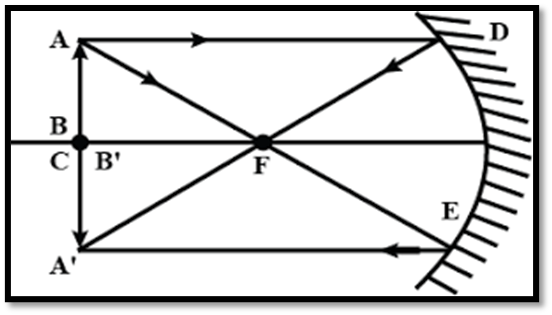
• Position of Object: At the Centre of Curvature
• Position of Image: At the centre of Curvature.
• Nature and Size: Real, inverted,same size as the object.

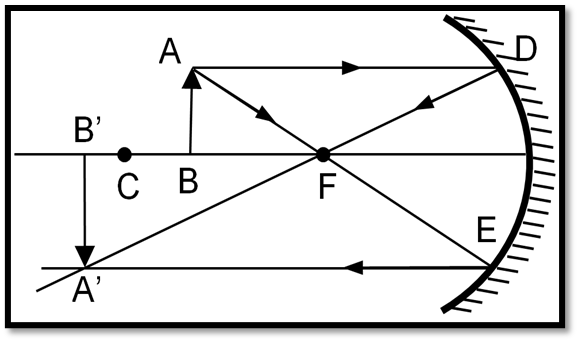
• Position of Object: Between Focus and Centre of Curvature
• Position of Image: Beyond the centre of curvature.
• Nature and Size: Real, inverted, and magnified.

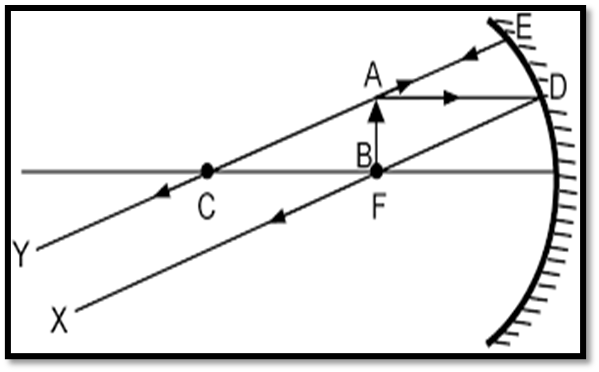
• Position of Object: At the Focus
• Position of Image: At infinity.
• Nature and Size: Real, inverted, and extremely magnified.

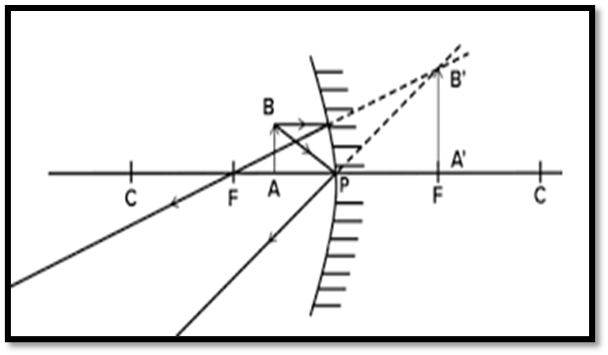
• Position of Object: Between the Pole and Focus
• Position of Image: Behind the mirror.
• Nature and Size: Virtual, erect, and magnified.

USES OF CONCAVE MIRRORS

• In torches, search-lights, and vehicle headlights for powerful beams.
• As shaving mirrors for larger facial images.
• By dentists for large images of teeth.
• In solar furnaces to converge sunrays and produce concentrated heat.

IMAGE FORMATION BY A CONVEX MIRROR

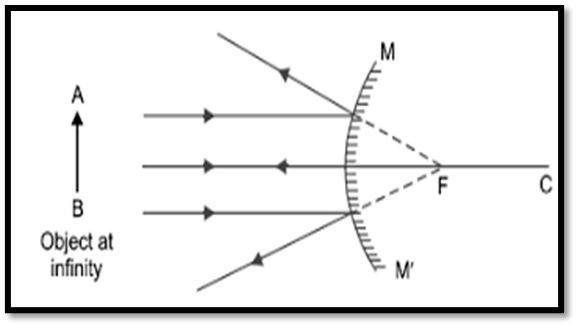
Position of Object: At Infinity

Position of Image: At the principal focus, behind the mirror.

Nature and Size: Virtual, erect, and extremely diminished.

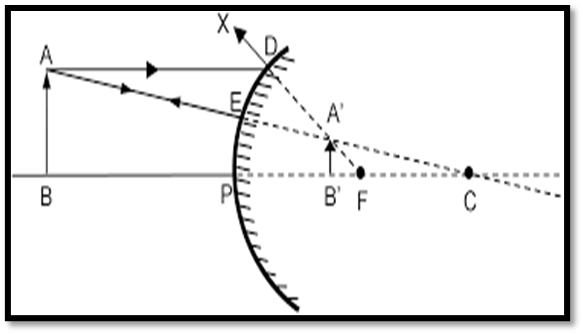
Position of Object: Between Infinity and the Pole (finite distance)

Position of Image: Between the principal focus and the pole, behind the mirror.

Nature and Size: Virtual, erect, and diminished.

USES OF CONVEX MIRRORS

• Rear View Mirrors: Used in vehicles for a wider field of view and always provide an erect image.
• Security Mirrors: Used in shops to monitor customers

SIGN CONVENTION FOR SPHERICAL MIRRORS

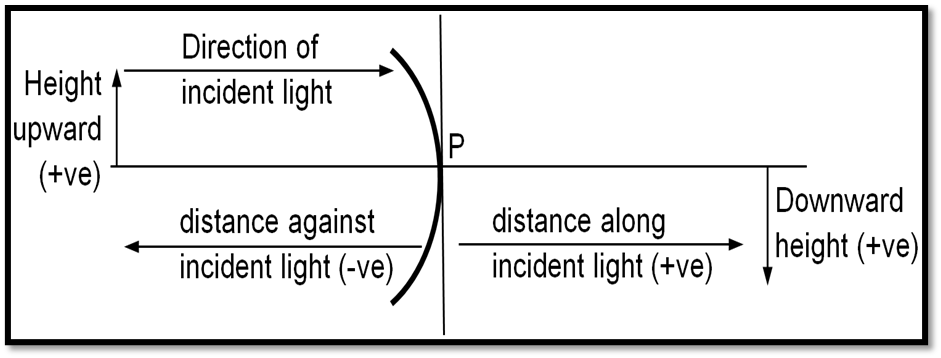
• It’s the set of sign convention that we should follow , also known as New Cartesian sign convention.
• The pole (P) of the mirror is the origin.
• The principal axis is the X-axis.
• Distances to the left of the pole are negative, and to the right are positive.
• Distances above the principal axis are positive, and below are negative.
• Focal length of convex mirrors is positive, while for concave mirrors, it is negative.

MIRROR FORMULA

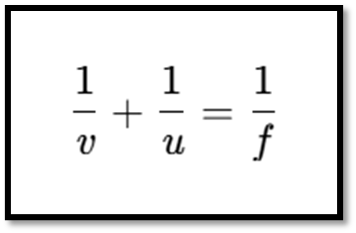
• Object Distance (𝑢): Distance of the object from the pole. Always negative.

• Image Distance (𝑣): Distance of the image from the pole. Positive if the image is virtual and erect, negative if real and inverted.

• Focal Length (𝑓): Distance of the principal focus from the pole.

The mirror formula is:

Magnification by Spherical Mirrors

Magnification (𝑚) is the ratio of the height of the image (ℎ₁) to the height of the object (ℎ_o).

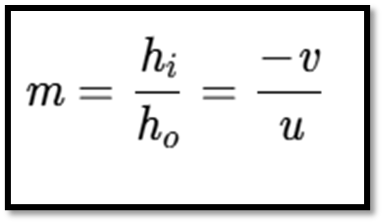
Magnitude: Indicates size relative to the object.

• m=1: Image is the same size.
• m<1: Image is smaller.
• m>1: Image is larger.

Sign: Indicates nature of the image.

• Negative: Real and inverted.
• Positive: Virtual and erect.

Magnification and Mirror Identification

Image Distance(𝑣):

• Can be positive or negative for concave mirrors based on object position.

Magnification:

• Positive and less than 1: Likely a convex mirror.
• Positive and more than 1: Likely a concave mirror.
• Negative: Always a concave mirror.
• Plane Mirror: Magnification is always +1.

Identification of Mirrors

Plane Mirror: Image size equals object size.

Convex Mirror: Image is diminished for all object positions.

Concave Mirror: Image is longer behind the mirror.

Focal Length: Independent of the medium.

Refraction of Light

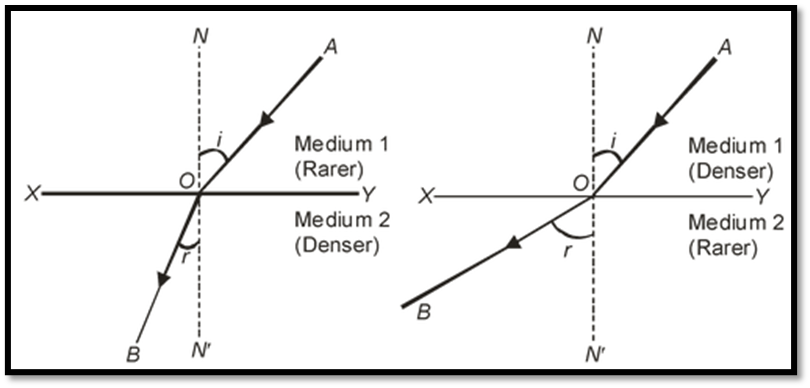
Refraction: Change in light path when passing between transparent media.

Angle of Incidence: Between incident ray and normal.

Angle of Refraction: Between refracted ray and normal.

Light Bending:

• Rarer to Denser Medium: Bends towards the normal (𝑖>𝑟).
• Denser to Rarer Medium: Bends away from the normal (𝑖<𝑟).

Cause of Refraction

• Optically Rarer Medium: Light travels faster.
• Optically Denser Medium: Light travels slower.
• Speed Difference: Causes refraction due to varying light speeds in different media.

Refraction of Light

Behavior:

• Denser Medium: Light bends towards the normal and speed reduces.
• Rarer Medium: Light bends away from the normal and speed increases.

Examples of Refraction

• A pencil in water looks bent.
• A lemon in water appears larger.
• The bottom of a pool looks raised.
• Letters under a glass slab appear raised.

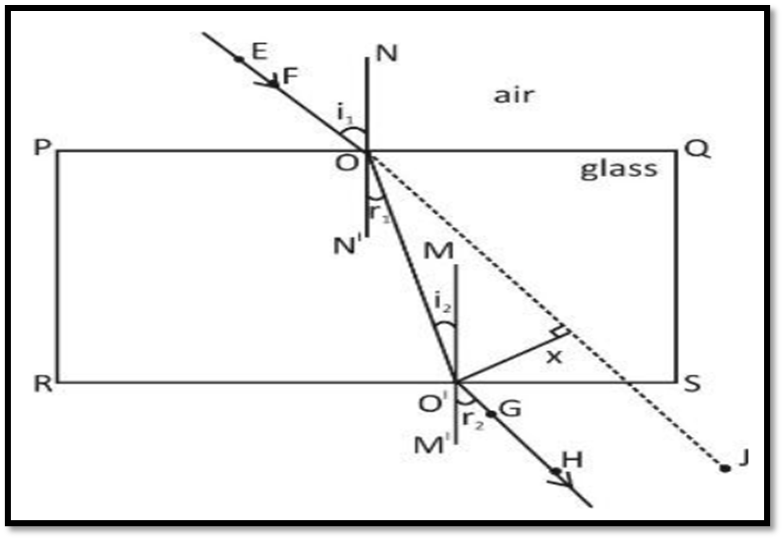
Refraction through a Rectangular Glass Slab

• The emergent ray is parallel to the incident ray but shifted sideways.
• Lateral Displacement: The perpendicular distance between the emergent and incident ray.

Important Points

• Angle of incidence equals angle of emergence (𝑖=𝑒).
• No bending if the ray falls normally on the slab.
• Greater deviation if speed difference between media is large.

Laws of Refraction (Snell’s Law)

Refractive Index

• Measures the change in light direction in a medium.

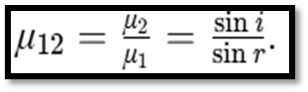
• Relative Refractive Index:
• Absolute Refractive Index: Compared to vacuum or air.

Note:

• Air has the lowest refractive index; diamond the highest.
• Dependent on material and light wavelength.

Refractive Index and Speed of Light

• Refractive Index (𝜇): Ratio of the speed of light in vacuum (𝑐) to speed in the medium (𝑣):

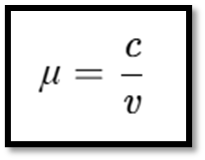
• Refractive Index of Second Medium: Ratio of velocities in two media.
• Refractive Index of Glass and Water:

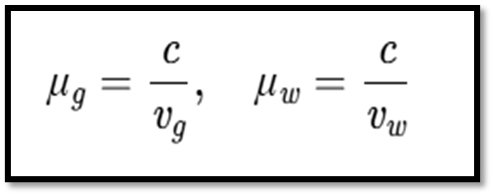
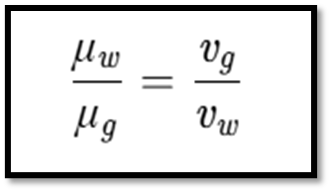
Absolute Refractive Indices of Materials

Different materials have specific refractive indices. For example:

• Water: 1.33
• Diamond: 2.42
• Glass: Varies with type (e.g., Crown glass 1.52)

Examples

• Example 1: Speed of light in diamond calculated using its refractive index.
• Example 2: Calculating angle of refraction when light enters water.

Lenses

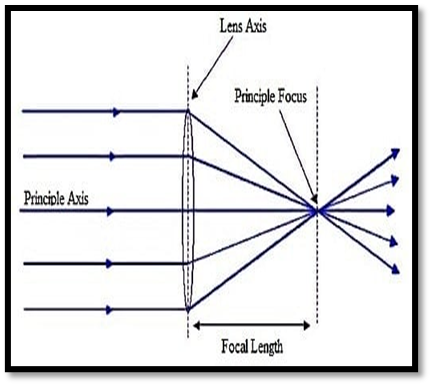
Convex or Converging Lens:

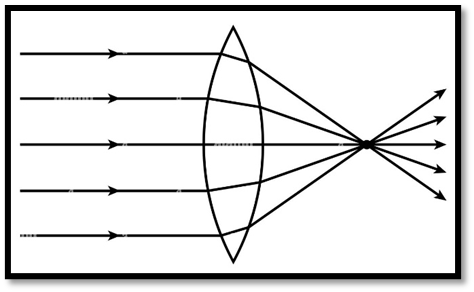
Definition:Thicker at the centre, thinner at edges.

Function:Converges parallel rays.

Concave or Diverging Lens

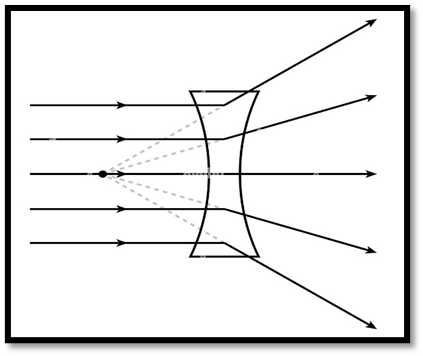
Definition: A lens thinner at the centre and thicker at the ends.

Function: Diverges parallel beams of light.

Definitions Related to Lenses

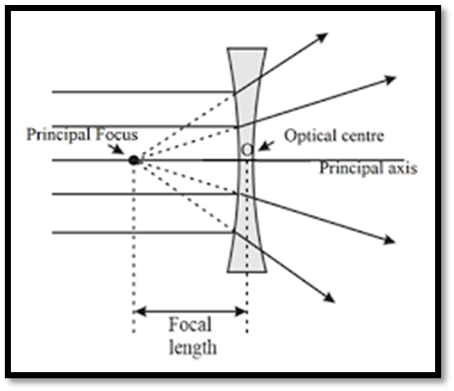
Optical Centre:

• The centre point of a lens, denoted by O.
• A point where incident rays pass without deviation.

Centres of Curvature:

• Centres of the imaginary spheres forming the lens’s surfaces.
• Denoted by C or 2F.
• A lens has two centres for its two curved surfaces.

Radii of Curvature:

• Radii of the imaginary spheres forming the lens’s surfaces.
• A lens has two radii, which may or may not be equal.

Aperture:

• Effective diameter of the lens’s circular outline.
• Represented by the distance MN.

Principal Axis:

• Imaginary line joining the centres of curvature.
• Passes through the optical centre.

Principal Focus

• First Principal Focus:Point on the axis where rays become parallel after refraction.
• Second Principal Focus:Point where parallel rays converge (convex) or appear to meet (concave) after refraction.

Focal Length: The distance between the focus and optical centre of the lens.

Focal Plane: A plane through the focus perpendicular to the principal axis.

Image Formation Using Ray Diagrams Ray Types for Diagramming:

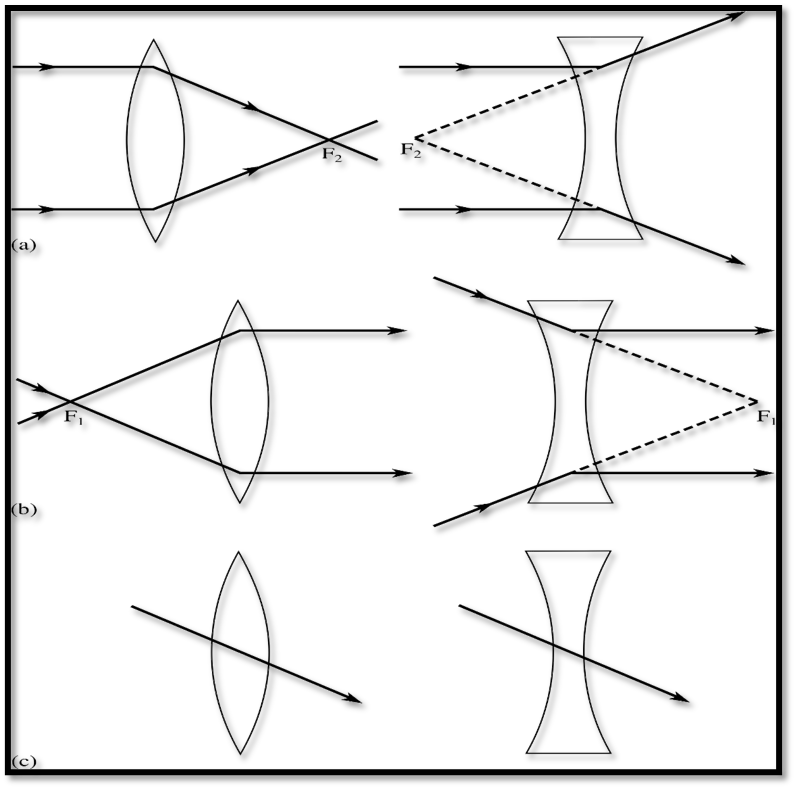
Parallel Ray: Passes through the principal focus after refraction in a convex lens or appears to come from the principal focus in a concave lens.

Focus Ray: Passes through or directed to the focus and emerges parallel to the principal axis.

Optical Centre Ray: Passes undeviated through the optical centre.

Formation of Images by a Convex Lens

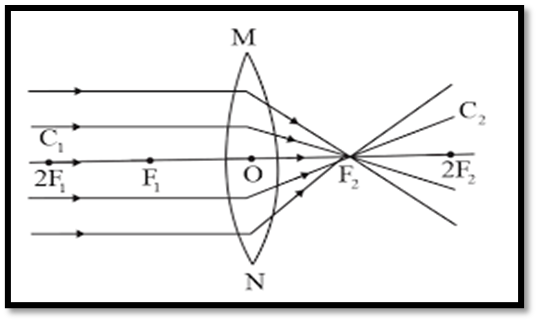
Object : At Infinity

Position of Image: At F₂

Nature and Size: Real, inverted, extremely diminished.

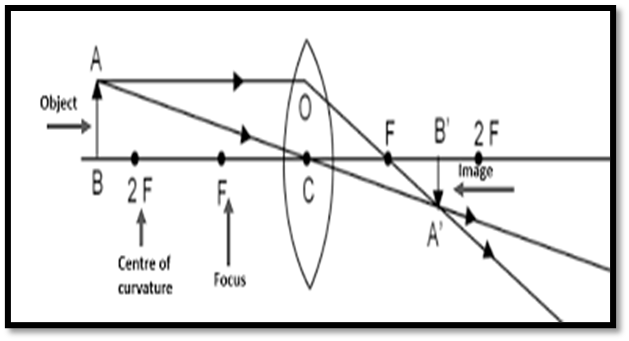
Object:  Beyond 2F _{1 ​}

Position of Image: Between F₂​ and 2F₂​

Nature and Size: Real, inverted, diminished.

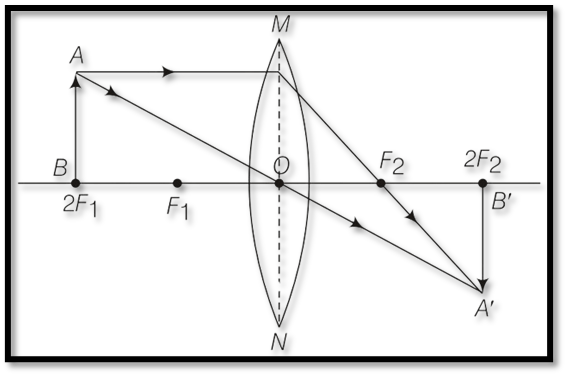
Object:At 2F₁​

Position of Image: At 2F₂

Nature and Size: Real, inverted, same size as the object.

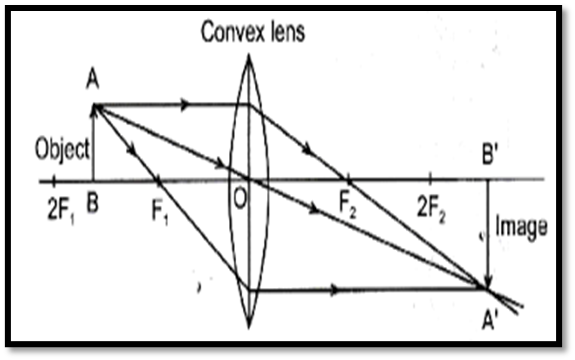
Object: Between F₁​ and 2F₁

Position of Image: Beyond 2F₂

Nature and Size: Real, inverted, magnified.

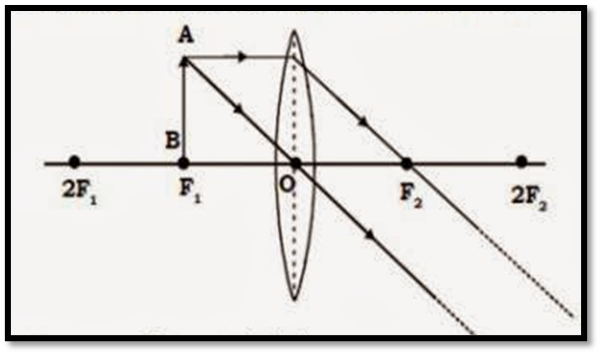
Object:At F₁

Position of Image: At infinity

Nature and Size: Real, inverted, highly magnified.

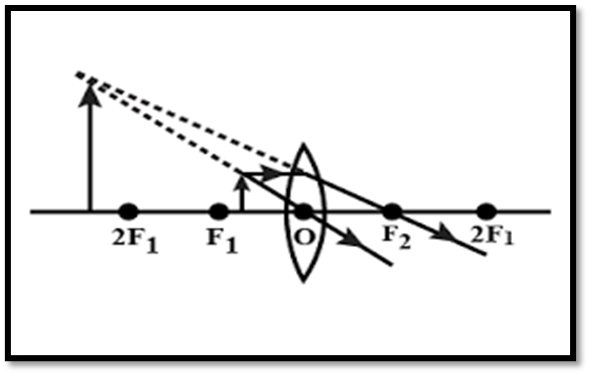
Object: Between Optical Centre O and F₁

Position of Image: On the same side as the object

Nature and Size: Virtual, erect, magnified.

Formation of Images by a Concave Lens

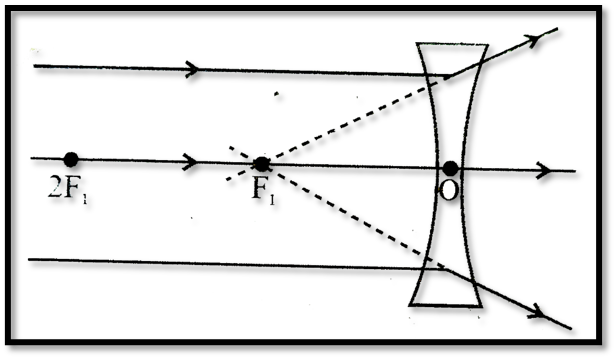
Object:At Infinity

Position of Image: At focus on the same side as the object

Nature and Size: Virtual, erect, highly diminished.

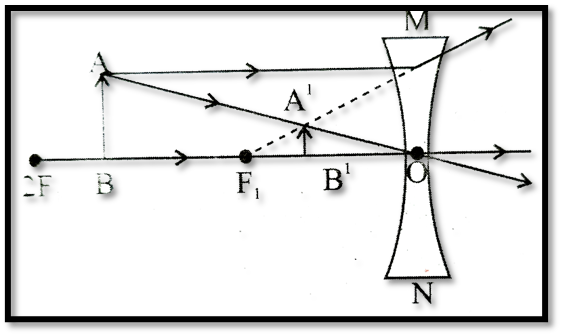
Object : At Finite Distance

Position of Image: Between focus and optical centre, on the same side as the object

Nature and Size: Virtual, erect, diminished.

• Sign Convention for Spherical Lenses
• Convex Lens:Focal length is positive.
• Concave Lens: Focal length is negative.
• Sign conventions are the same as those for mirrors.

Lens Formula:

Magnification by Lenses Formula:

The ratio of height of image  (h₁) to the height of object (h_o) is called Magnification (m)

​ Sign:

• Positive for virtual images
• Negative for real images

Power of a Lens

The ability of a lens to converge or diverge light rays is called Power of Lens. It is defined as reciprocal of Focal length.

If f is expressed in m, then power is expressed in dioptres. One dioptre is the power of a lens whose focal length is 1 m. if focal length is in cm, then ,

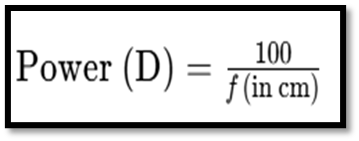
Sign Conventions:

• Concave Lens: Negative power and focal length.
• Convex Lens: Positive power and focal length.

Power of Combination of Lenses

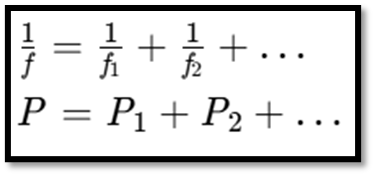
• When using multiple lenses, the equivalent focal length ( f) and power ( P) are calculated as:

Magnification (m):

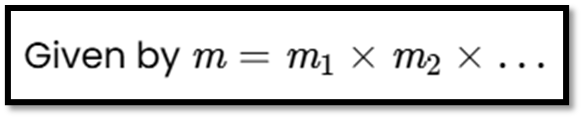
• Using combinations of lenses can improve image sharpness and reduce defects.